囲碁の恒等式とダメ~な~理論

囲碁の恒等式とダメ~な~理論　
　　　　　　　　　入澤　元

理論１

この理論の真偽を実戦で証明したいのですが、私は何しろ簡単に間違えるものですから、その真偽を実戦の成績で私の棋力、手筋の力では証明しようがないのです。そこで、普通の打ち方と変な打ち方を試みて、同じ程度の勝率なら証明の傍証になると思います。そんな狙いをもって、間違えないように考える時間がたっぷりあり、棋譜が残るメール囲碁をしてみることにした次第です。（モルモットにされた方には気の毒ですが。）棋譜が残るので、間違えなかったケースを見れば、新理論が有効か、きっと判定ができると考えたからです。もっとも、せいぜい同じ程度の勝率なら、既にお馴染みの布石で済むわけだから、これは明らかに徒労というものです。同じ時間を使うなら定石を覚える方が強くなれるに決まっています。しかし、そこは一つでも判明したことをベースとして何かを発展させるのは、ヒマな人間の務めと心得て、挑戦してみた訳です。囲碁好きの私の従兄弟には、囲碁は楽しむもので、理論を考えるものではないと一蹴されました。この私の囲碁理論に関する真偽不明のもやもやとした悩みは、昨年の初めニンテンテンドーＤＳの銀星囲碁ソフトで遊んでいる時に始まりました。囲碁にはある恒等式あるいは条件式があることに気がついたのです。
ケインズ経済学などというものも唯一本の恒等式（国民所得は国民総生産と投資の和と事後的に等しいという事実）から始まるのですから、この恒等式プラス「いつも対局者と同じ価値の手が必ずある」という前提が最後まで守られるということから分かることは何かと考えてみたわけです。（深読みし過ぎて、間違えたかも知れません。）
この式ではダメの数を未定として考え、囲碁とはダメがゼロになるまでのゲームであると考えると理解しやすいので、ＤＳ（dead space)理論という名前をつけました。理論だけでは信憑性に欠けるので、いろいろと実例を集めて、今年の３月に小論にまとめたものです。但し、実例を集めようにも、大概の人には変な打ち方として敬遠されるので、実例として集めた相手は文句を言わないＰＣソフトです。ＰＣソフトは全く弱いのですが、同じ反応を示すので、経験から傾向を読めるのがメリットです。これらは手筋ベストとは到底言えないので、これが人間相手の実戦に通用すると考えないでください。また、当然のことながら、これが正しいと唱えるには、私程度の棋力によっては何ら実践的裏付けがありません。（つづく）

理論２

私が考えてみたことは、次のような疑問に関して何か答えがないだろうかということです。
①　囲碁は本当に無限に複雑なゲームか？三劫などの循環になるケースは終りがないが、普通は着々と手数に従って、様相が一定の方向に変わるのであって、それほど複雑ではないのではないか？
（手数４０の倍数を指標として様相が変わる！（注）参照　）
②　１９路盤の布石は何故隅の星、小目、３三などから始めなければならないのか？５路盤では天元から、７路盤でも天元から打つのが有利なのに、不思議と思いませんか。５路、７路、１３路、１９路に共通する布石理論がないのだろうか？（星に合理的な理由があるのと同じくらい合理的な位置が天元に近いところにもある！　隅から局地戦
を始める以外に、中央から同じ程度の戦い方ができるはずだ！多分、５七、６七などが合理的！）
③　１９路盤では盤を石で埋めていく間に、いつも相手の手と同じ価値のある手を打つことができれば
初手や数個の置石の価値が最後にコミとなって残るのではないか？すると、いつも相手と同じ価値の手
があるというのは正しいだろうか？
（プラスの価値だけでなく、相手に損害を与えるマイナスの価値も含めて考えれば、均して同じ価値の手がある！）
④囲碁で同じ価値の手というのは、打つ時に分かるものか？
後から打った手で前に打った手の価値が上がったり、下がったりするのだから、分かるはずがない。
しかし、碁盤に対称性があるから、同じ価値の手を捜すことはそんなに難しくないのではないか。
（単調に一手の価値が減るとかいうのではなく、布石の初期の一手の価値は６から７目だが、複数の石の関係で一手の価値が増えていって、最後は最小の価値になる！）
⑤ダメから囲碁を見ると分かり易いのではないか？
（石の間隔が空く程、多くのダメが発生する！　ダメが多く発生させる＝敵の地を減らすのが良い打ち方！ダメの配達を確保する打ち方を考える。アンパンの皮のように、ダメが多くできるように、アンコをなるべく遠巻きにする！）

例などもついた全文は、PDF文書です。興味のある方は覗いて見てください。但し、これを読んだ結果、囲碁の調子が狂って弱くなることは十分予想されますが、私はその責任は負いませんので、予めお断りしておきます。

理論３

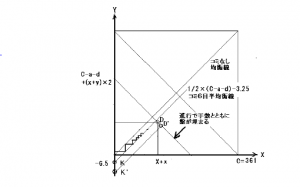
以下に、囲碁の恒等式、その図解、囲碁ゲームの総合利得、戦略と戦術に分けて小論からピックアップします。
１．　スペースの恒等式
まず、囲碁の恒等式とその直接的な意味を整理してみる。
C－a + x + y = X + Y + d
ここで、Cは碁盤の大きさであり、19路盤では361の交点＝361の目がある。
a は進行手数であるが、パスの回数を除く。
Xは黒の地、Yは白の地、xは黒のアゲハマ、yは白のアゲハマの数である。ｄは最後まで未定であるが、ダメの数で、ダミー変数である。
左辺は、碁盤上のスペースは361から始まり、打った手の数だけ減り、アゲハマの数だけ増えることを示す。一方、右辺は、スペースが黒地と白地とダメに分けられることを示す。 但し、ダメは、線型計画法のスラック変数のようなもので、左辺と右辺のバランスを取るための余りを示しているに過ぎない。ダメが最終的にゼロになった時に、初めて黒地、白地が確定されるが、その時までは、見込みに過ぎない。
上の恒等式は、ゲームのどの段階でも必ず成り立つ恒等式である。どんな段階でも、即ち、ダメが残っている段階でも、ダメを埋めてダメの数がゼロになった段階でも、常に成り立つ。ニンテンドーDSで9路盤の囲碁をやっていて、全部石を取った時に成り立っている最終状態では、単純に黒地または白地だけになった。実はこの関係式は、そのような特殊なケースだけでなく、途中の状態についても成り立つように工夫したものである。当然既に多くの人が経験的に気づいているはずである。
この囲碁の恒等式は、至極単純に言えば、全く当然のことであるが、手数が進むほど、黒と白が分ける盤上のスペースの大きさが減るということである。もちろん例外として、大石が死んだ場合、アゲハマの数が増加して、その跡地の盤のスペースが増える一時的な現象が起きる。 しかし、そこから残りのスペースが再び減っていく。つまり、性格として言えば、一手ごとに減っていく碁盤のスペースに関する恒等式である。
この恒等式のＸとＹの関係を用いて勝敗の決定式を求めることができる。ここで、コミは６目半とする。
Ｙ－x ＞ (Ｃ－a －d)／２　＋3.２5　（白優位）
Ｘ－y ＜ (Ｃ－a －d)／２　＋3.２5　（黒優位）

上式の意味することは、
①　囲碁はダメの数d がゼロになるまで手数 a（パスの回数は除く）が進行する。但し、全てのダメの確定は最後になるので、その時まで、ダメの数 d はおおまかに分かるとしても、あくまでも未知数である。

②　勝敗（両者の地の差Ｙ+ｙ-Ｘ-ｘ）は、実質的な地の大きさ（白は（Ｙ－ｘ）、黒は（Ｘ－ｙ））が潜在的地の均衡分岐点をどの程度越えたかということである。

つまり、勝敗は、（イ）自分の地、（ロ）取られた石の数、（ハ）進行手数、（ニ）ダメの数で決まる。（敵の地と自分が取った石の数によらない表現であることに注意）。ここで、（イ）－（ロ）は自分の実質の地である。 （注）上の式の a 進行手数とは、パスの回数を除いたものである。

２．スペースに関する恒等式の図解
１で示したスペースの恒等式は、　「盤の黒地、白地とダメの数の総和は、盤の目の数から打った石数を引き、死んだ石数（揚げた石数＋揚げなくても取られている石数）を加えた数と等しい。」である。

Ｘ＋Ｙ＋ｄ＝Ｃ－a＋ｘ＋ｙ
ここで、Ｘ，Ｙ：　黒の地、白の地　
　　　　ｘ, ｙ：　黒が取った石、白が取った石

a：　パスを除いた進行手数
d：　ダメの数　ダメの数は最後に詰めてゼロになるが、その時までは確定できないパラメータないしスラック変数

以上の関係を、例によって、図にしてみる。
（１）下図は、黒と白の地やアゲハマの状態をＸＹ座標図で示している。
黒地Ｘ＝ 47、白地Ｙ＝ 40の交点が点Ｓである。

地のトータル 40＋ 47＝ 87は、目の数 361　マイナス　手数 304、ダメ16　プラス　アゲハマ計 46　と等しい。これは、盤上のスペースが、「361マイナス置いた石プラス上げた石」であるということである。これに黒、白、夫々にとったアゲハマを足した点が、87 プラス 46＝133の線上の点　Ｄ右上であり、夫々にとられたアゲハマを引いた数が、87 マイナス 46＝ 41の線上の点　Ｄ左下である。
この点の座標の差が勝敗であり、コミ-6.5の線の右にあるから、黒が勝ちである。
そのポイント差は（70－63）または（47－40）で７目、コミ６目半で黒半目勝ちである。

  　進行図

＜＜　囲碁は上のような二等辺三角形がだんだん縮んでいき、ダメがなくなって終わる。手が進む間、対局者の利得の座標は三角形の中を漂流する。石が独立の地位を持つように２間離れるような3×3のスペースは40個盤上に取れるのだが、その中に一手ずつ石を散らばせていくと、石の密度に従って様相が進化していく。80手で布石が終り、120手で形勢が決まることがある。160手で勝負が偏らなければ、寄せが続いて劫などがなければ240手で終わる。隙間が 361マイナス 240≒120とすると、黒と白が64対56くらいで分かれることになる。＞＞ （つづく）

囲碁ゲームの総合利得

囲碁で一手ずつ最善と思われる手を応酬する過程は分かった。それでは、多数の手が続いた後の黒と白の夫々のゲーム総合の利得あるいは勝敗はどうなるか。

H ( a( i ) | { a ( i － 1 ) } ) = τ( i ) { ( X + x ) － ( Y + y ) } を i が奇数の場合（黒）と偶数の場合（白）に分けて、最初から最後まで足せば、夫々の利得総計であり、コミが適正に決まっているとすれば、黒としては、この利得総計がコミを越せば勝ち、越さなければ負けである。

連続関数では ｆ（ｘ）＝ｇ（ｘ）の時 ∫ｆ（ｘ）ｄｘ＝∫ｇ（ｘ）ｄｘ＋Ｃ　（定数）である。

この定数は初期条件、境界条件で決定される。

囲碁の場合は、離散形の利得の集計である。第一手を除き、黒と白が続けて打っていく手の利得はならせば各回同じである。何故なら、両者が間違えなければ、交代してお互いにプラスとマイナスの利得を与え合うので、碁盤が大きければ等価の手が十分最後まで存在する。
従って、黒の利得総合は、
Ｓ = Σ｛δ{ ( X + x ) － ( Y + y ) } ｝＝　
｛　Σ｛τ( i ) δ{ ( X + x ) － ( Y + y ) } ｝｜奇数　｝マイナス
｛　Σ｛τ( i ) δ{ ( X + x ) － ( Y + y ) } ｝｜偶数　｝＝
｛τ( １) δ{ ( X + x ) － ( Y + y ) }｜i =1 　（初手の価値） ＋
Σ ｛ τ( k ) δ{ ( X + x ) － ( Y + y ) } －　τ( k+1 ) δ{ ( X + x ) － ( Y + y ) } 　｝｜k = 偶数

　　（以降の手のペアの価値の差総計） ＝　定数k は二百手から三百手に及ぶので、シグマの最後の項は１か０で終り、それは、盤上に石が詰まっていく最後のところでダメの残り具合で黒になるか、白になるか予想はできないが、均せばゼロであろう。
この定数がコミであり、コミについて予想したように、第一手では敵に与える最小でもδ（－Ｙ）＝６目か７目のダメ放散能力である。第一手は碁盤の上の小さな渦巻きのようなもので、その周りに損得なしに黒と白が交代して石を置いていくことができる。最初の渦巻きは、それを避けて打つことができる。
しかし、その影響が次の渦に移り、生まれた渦が最後まで消えないようなものではなかろうか。

大きな盤では、何個か置いても、同じように渦巻きがいくつかできて、その周りで損得なしのゲームが行われるので、置石の数に比例してコミがつくというような経験側が自然に成り立つことになるのだろう。

＜＜　小論には書いてないが、各回の利得を左右する項目別に整理すると、次のようになる。
　単項目の効果
　主に寄せに入ってからの狙い
　δX ：　締り
－δY ：　敵の地を荒らす
　δｘ ：　切取り
－δｙ ：　繋ぎ（取られる石を減らす）

　複項目の効果
　序盤から中盤では複合的な狙い
δ（X－Y） ：　模様の拡大、模様の接点での競り合い
δ（X＋ｘ） ：　包囲して取る。取って根拠を確保する。
δ（X－ｙ） ：　取られそうな石を繋ぎや渡りで、本体に連絡して、犠牲 δｙ をゼロにする。
δ（X－Y－ｙ） ：　捨石 δｙ プラス抜き跡の地 δY より多く（２δｙ 以上）の地を増やす。
δ（ｘ－Y） ：　敵の地になりそうなところに、打ち込み、敵の石を取って、勢力を伸ばす。
δ（－Y－ｙ） ：　繋ぎや渡りで、犠牲 δy をゼロにしつつ、敵の地を消す。　
δ（ｘ－ｙ） ：　切られたところ δy を生きる。または、切って取る。　

　　＞＞